 In the horizontal plane the only force acting is a drag force (Fx)
so we have:-
In the horizontal plane the only force acting is a drag force (Fx)
so we have:-Having presented computer models which are presented as modelling arrow flight it only fair to outline the methodology used in the models so anyone using them have some idea on what basis they work and all the simplifications/limitations of the approach taken. The following therefore presents an overview of the models in general and specific aspects for the 2D and 3D models.
A cross sectional area a angle of arrow to the horizontal Cd Drag coefficient D Air density F drag force (suffix denotes direction) f constant acceleration (suffix denotes direction) g gravitational acceleration I arrow moment of inertia at point of arrow rotation L distance of centre of pressure to point of arrow rotation m mass of arrow t time v arrow velocity (suffix denotes direction) x horizontal distance y vertical distance
The starting point to look at the behaviour of a 'mechanical' system is Newton’s equation
mass x acceleration = forces applied.
In a two dimensional model three equations are required to define the arrow flight the horizontal (x) acceleration, the vertical (y) acceleration and the rotational (a) acceleration.
 In the horizontal plane the only force acting is a drag force (Fx)
so we have:-
In the horizontal plane the only force acting is a drag force (Fx)
so we have:-
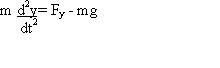 In the vertical plane the forces acting are gravity (mg) and a drag
force (Fy) so we have:-
In the vertical plane the forces acting are gravity (mg) and a drag
force (Fy) so we have:-
 Rotationally the force acting is the torque resulting from the total
pressure (drag forces plus Munk moment) acting at the centre of pressure
so we have:-
Rotationally the force acting is the torque resulting from the total
pressure (drag forces plus Munk moment) acting at the centre of pressure
so we have:-
For a 3D model you would have two additional equations, one for acceleration in the third (z) direction and one for the angular acceleration in the xz plane.
Because of the dependency of the drag force on the square of the velocity it is not possible to get an analytical solution to the above equations e.g. you cannot derive an equation which gives you the height of the arrow as a function of horizontal distance.
The drag forces on the arrow change gradually over time, no sudden changes. If you take a small time interval then the change in drag force over the time interval will also be small. The shorter the time interval the smaller the change in drag force. With a small enough time interval the drag force can be regarded as being constant over the time period. If the drag force is constant then the acceleration resulting from the drag force is constant.
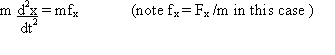 If we have a small enough time period then the equation for acceleration
is the horizontal plane can be written as:-
If we have a small enough time period then the equation for acceleration
is the horizontal plane can be written as:-
This equation is solvable. Integrating and rearranging we get:-
dx = vx = c + fx t
dt
At time t = 0,
vx = c
therefore the
change in velocity over time t is given by fx t
Integrating again we get:-
x = c + vx t + fx t2/2
At time t = 0, x = c
Therefore the change in position over time t is given by vx t + fx t2/2
The above process can be similarly applied to accelerations in the 'y' and 'a' directions.
If we can calculate the forces Fx, Fy, Fa at particular instant in time, and hence the corresponding accelerations, then we can calculate the positions and velocities at a subsequent time as long as the time interval is short enough so that the drag forces do not vary significantly. The starting point is when the arrow leaves the bow where we define the initial positional and velocity values. The three accelerations (x,y,a directions) are calculated. The new positional and velocity values are calculated after a short time. These new values are used to recalculate the accelerations to apply over the next time interval and so on.
By trial and error you find the time interval short enough so that any shorter time does not make any practical difference to the calculated arrow flight properties at the resolution you want (one metre horizontal distance in the case of the two models). This time interval turns out to be around one thousandth of a second.
If you take a typical target arrow flight time as 2 seconds it means that to calculate say a trajectory means doing around 2000 sets of calculations. This is why before the advent of the computer, modelling arrow flight was not a practical proposition. (To get some idea of arrow flight behaviour people did make drastic simplifications to get an analytical solution. However these analytical models do distort the picture e.g. no need to 'match arrows' or 'tune' a bow).
The forces we need to calculate to determine the accelerations for basic model described above are gravity, drag and the Munk moment.
At the height we shoot arrows the gravitational force can be assumed constant so no problem with this. This leaves the aerodynamic effects.
With the typical range of arrow speeds (150-350 feet per second say) the air can be regarded as incompressible and the air flow over the arrow regarded as laminar. The approach taken in calculating drag forces is that of using a drag coefficient Cd.
The drag coefficient is defined as the ratio of the total drag to the dynamic pressure of the flow i.e.
F = 0.5 Cd D A v2
where 'D' is the fluid density, 'A' the frontal exposed area of the body and 'v' the overall fluid velocity normal to the surface 'A'.
The density of air is around 1.2 gms/litre (you can correct for temperature, relative humidity etc. as you wish, in both models this is a direct input). The air density is assumed constant irrespective of arrow altitude (so don't try modelling an arrow that goes up thousands of feet!)
The appropriate value of 'A' (ref. pile shaft or fletchings) is assumed known from the properties of the arrow. Arrow shafts are assumed parallel so the area per unit length is constant along the shaft (the models do not cater for barrelled shafts). The pile area is assumed to be the cross sectional area of the shaft. In the 3D model the fletching area is entered as a fixed quantity, this area is assumed to be located 5 cm from the nock end of the shaft (the assumed centre of pressure). In the 2D model the fletchings are assumed to be right angled triangles at a specified position. ( The centre of pressure is calculated).
The drag forces with respect to velocity are calculated in the models in a co-ordinate system based on the arrow. For the 2D model the drag forces along the arrow axis and the drag force normal to the arrow axis are calculated (In the 3D model you have an additional drag force normal to the other two). The axial drag force (related to moving the arrow) is derived from drag on the pile and the edges of the fletchings. The normal drag force(s) (related to moving the arrow) is derived from drag on the relevant section of the shaft. The normal drag force(s) (related to rotating the arrow) are derived from the drag on the fletching surfaces and from the relevant part of the shaft. It is assumed that drag on the pile acting to rotate the arrow is negligible ( so modelling broadheads is not an option). In the 2D model the shaft normal air velocity is assumed to act at a 60 degree angle to two fletching surfaces.
As an arrow is rotating during its flight the air velocity will vary along the arrow shaft and hence the drag forces will vary along the shaft. This effect is neglected in both models as with 'good flying arrows' the effect will be small. The basic result from this approximation is that the damping of arrow fishtailing/porpoising will be calculated to be smaller then it actually is.
As far as applying drag coefficients in calculating pile, shaft and fletching drag forces it's basically pick a number time. The only practical way to get values for drag coefficients is to conveniently have a wind tunnel available to measure them. One saving grace is that over the velocity range of typical arrows the drag coefficients will be fairly constant. For a long cylinder (arrow shaft) the drag coefficient will be somewhere around 1.2. For the variety of pile configurations probably somewhere around 0.4 (applying bullet drag coefficients to arrows is a bit iffy as bullets tend to be going a bit quicker than arrows). For the fletchings a drag coefficient value of around 2 (maybe).
The second aerodynamic effect is the Munk moment which generates a rotational torque on the arrow. The reason it is included in the models is that it has a significant effect on arrow flight in some cases i.e. bareshaft arrows with low FOC or flight shooting. As with drag coefficient the only realistic way to get at the Munk moment is to use a wind tunnel as the moment depends on the nock geometry. In the 3D model the Munk moment is estimated by relating it to the area of the shaft contributing to arrow rotation (basically so you can make the arrow rotate one way or the other to see what happens). In the 2D model the Munk moment is defined as a 1.5 cm area acting at the nock. (you can roughly estimate the Munk moment on an arrow by doing a walk back with a bareshaft arrow varying the FOC until the torque from shaft drag balances the torque from the Munk moment, the pattern curvature switches over)
In conclusion based on the calculation of gravitational force and the aerodynamic forces as described above the values of the accelerations fx, fy and fa can be calculated at any point to apply to positional and velocity changes over the next time interval.
If you want to look at the effect of bow tuning or a variation in the quality of the archer's shot on how the arrow flies then you need to define to the model appropriate initial arrow properties to reflect these effects. The two relevant properties are the initial arrow orientation and the arrow angular velocity. These are handled differently in the two models as described below.
The 2D model is the simplest. The angle 'a' at which the arrow leaves the bow is assumed to be the bow angle. The parameter you can vary is the angular velocity the arrow has in the vertical plane when it leaves the bow. The value you enter under 'tuning' is the initial angular velocity (in tenths of radians per second) , pile going up or down as required.
In the 3D model the initial angular velocity is related to the initial arrow angle. The initial arrow angle (in the vertical and the horizontal planes) is the sum of the bow angle (flight set up), the angle related to the tuning of the bow (tuning set up) and the angle related to the quality of the shot (archer group set up). There is an internal routine which calculates the initial arrow angular velocities in the vertical and horizontal planes based on the difference between the arrow angle and the bow angle. The relationship between this difference in angle and the arrow angular velocity can be scaled using the rotation coefficient. e.g. If you want to model an arrow leaving the bow at an angle to the bow angle but with zero angular velocity then the rotation coefficient should be set at zero. Alternatively if you set the tuning angle very small and the rotation coefficient very large then you effectively have the same situation as the 2D model - the arrow leaves the bow at the bow angle but with angular velocity.
Last Revision 1 July 2009