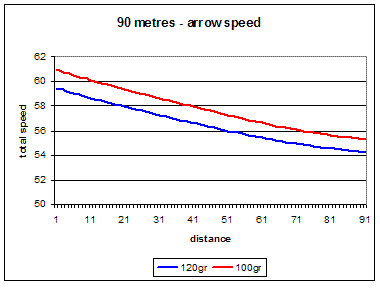
 For the first assessment the two arrows are perfectly shot at a 90 metre target distance and the
'Flight' simulator used to generate the total arrow speed over the distance.The following graph compares
the speed over distance for the two arrows.
For the first assessment the two arrows are perfectly shot at a 90 metre target distance and the
'Flight' simulator used to generate the total arrow speed over the distance.The following graph compares
the speed over distance for the two arrows.The frequently heard expression of the form "A heavier arrow retains its energy at longer distances", usually implying e.g. that a heavier arrow will be travelling faster at 90 metres than a lighter arrow, is one of those awkward archery myths because the statement itself is true. It's only the understanding of the phenomenon and it's practical effect on arrow flight behaviour that is incorrect.
Using the 'Flight' arrow simulator I will try to put over a sensible interpretation of the comment.
The approach is to compare the flight characteristics of two arrows. Both arrows are 29" X10 650 shafts with identical fletching and nock assemblies. The only difference is that one arrow has a 100 grain point and the other arrow has a 120 grain point. It is of course impossible in real life to change only one variable for an arrow so the assumed arrow properties are:
100 grain pile
120 grain pile
The different arrow properties are fairly consistent with a 20 grain difference in point weight.
 For the first assessment the two arrows are perfectly shot at a 90 metre target distance and the
'Flight' simulator used to generate the total arrow speed over the distance.The following graph compares
the speed over distance for the two arrows.
For the first assessment the two arrows are perfectly shot at a 90 metre target distance and the
'Flight' simulator used to generate the total arrow speed over the distance.The following graph compares
the speed over distance for the two arrows.
The lighter arrow has the higher launch speed and with increased distance the gap between the two arrow speeds decreases partly (mainly?) because of the effect of the mass difference on the relative arrow accelerations. However in this case at 90 metres the lighter arrow still has the higher speed.
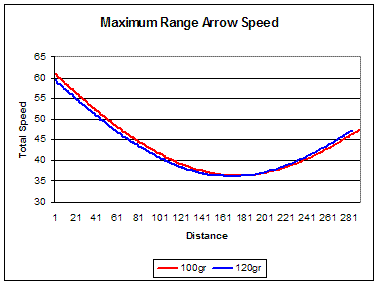 For the second assessment the two arrows are perfectly shot at an angle to reach maximum distance
and the 'Flight' simulator again used to generate the total arrow speed over the distance.The following
graph compares the speed over distance for the two arrows.
For the second assessment the two arrows are perfectly shot at an angle to reach maximum distance
and the 'Flight' simulator again used to generate the total arrow speed over the distance.The following
graph compares the speed over distance for the two arrows.
The lighter arrow has the higher launch speed and with increased distance the gap between the two arrow speeds decreases partly (mainly?) because of the effect of the mass difference on the relative arrow accelerations. At around 187 metres both arrows have the same speed. At longer distances the heavier arrow has a higher speed. (In case you are wondering the arrow speed is increasing during the latter part of the flight because the arrow is 'falling down' and accelerating under gravity. The speed gain from this is greater than the speed loss from drag). Worth noting that the maximum range of the lighter arrow is about 7 metres greater than the heavier arrow.
You can see from the above simulation that 'the heavier arrow retains its downrange energy' statement is true and the corollary that the heavier arrow will end up travelling at a higher speed is also true. Where these correct facts are misleading is that you have to be shooting a lot further than 90 metres for this effect to become a practical reality.
Why do so many people get this relationship between overall arrow mass and speed variation wrong? My guess is that what people look at is the speed difference between different arrow shafts of which the difference in overall mass is only one of a large number of variables and they happen to 'pick' the one of lower relative significance.
So let's repeat the above assessment using this time three different shafts, the X10 650 as above and equivalent ACE 670 and Navigator 610 shafts. All arrows have identical point (100 grain), nock and fletching assemblies. In this case the respective arrow parameters are:
X10 650
ACE 670
Navigator 610
The differences in arrow mass are similar to the 20 grain difference we chose for the X10 shaft comparison. Need now of course to include the arrow diameter as a variable.
It is clearly impossible to define how much individual arrow components or individual arrow properties contribute to the overall arrow drag and hence to arrow speed variation. However I think you can reach some plausible views.
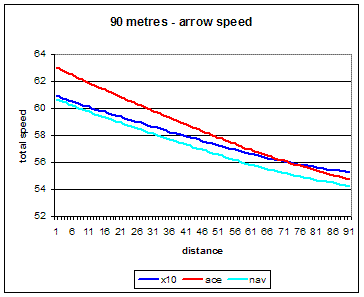 For 90 meters distance starting off with the X10 versus the Navigator they both have similar overall
masses,launch speeds and FOC values but the Navigator loses speed much faster than the X10. This
supports the X10 comparison above in saying that although overall mass has an effect on speed loss
it's a relatively minor contributor. The big difference between the two shafts is the smaller diameter
of the X10 which for sure is going to result in less drag slowing the arrow up. Highly suggestive that
diameter is a major player as regards speed loss.
For 90 meters distance starting off with the X10 versus the Navigator they both have similar overall
masses,launch speeds and FOC values but the Navigator loses speed much faster than the X10. This
supports the X10 comparison above in saying that although overall mass has an effect on speed loss
it's a relatively minor contributor. The big difference between the two shafts is the smaller diameter
of the X10 which for sure is going to result in less drag slowing the arrow up. Highly suggestive that
diameter is a major player as regards speed loss.
Whereas when comparing the two X10s above the lighter arrow had a higher speed at 90 metres, in this case the X10 speed overtakes the ACE speed at around 70 metres. While the higher FOC of the ACE will make a contribution to increased drag slowing the arrow up the FOC difference is less than the case for the two X10 arrows so again it seems that the smaller diameter of the X10 is the key property as regards speed loss between the X10 and the ACE.
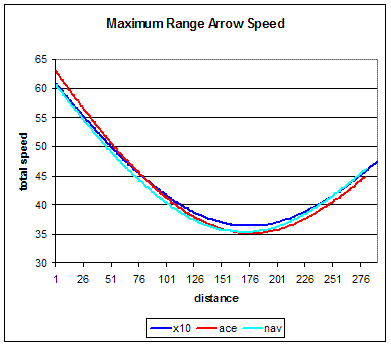 While it doesn't add much to the argument for completeness sake I've included the speed variation
for the three arrows shot at maximum range. As regards distance the X10 goes the farthest distance,
the ACE the shortest, and the Navigator is between the two. That the maximum range is in the same
sequence as the arrow diameter may or may not be a coincidence (always more questions :) ) but clearly
the maximum range does not match the sequence of overall arrow masses. The X10 speed overtakes the
ACE speed before the Navigator speed overtakes the ACE speed, again raising a flag that diameter may
be the the dominant parameter.
While it doesn't add much to the argument for completeness sake I've included the speed variation
for the three arrows shot at maximum range. As regards distance the X10 goes the farthest distance,
the ACE the shortest, and the Navigator is between the two. That the maximum range is in the same
sequence as the arrow diameter may or may not be a coincidence (always more questions :) ) but clearly
the maximum range does not match the sequence of overall arrow masses. The X10 speed overtakes the
ACE speed before the Navigator speed overtakes the ACE speed, again raising a flag that diameter may
be the the dominant parameter.
Drag affecting properties like FOC have much more of an effect at longer distances so any interpretations are going to be a lot less clear cut than at shorter distances.
Last Revision 1 July 2009