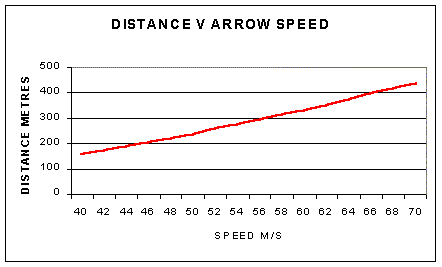
The higher the speed at which the arrow leaves the bow then the
farther it goes. No surprises there. We need a bow with a high potential
energy storage in the limbs and an efficient use of this stored energy in
creating a high speed arrow.The aim of flight shooting is to shoot an arrow (into the ground) as far as possible. I have no practical experience of flight shooting, always a good place to start, but it's possible on a purely mechanical basis to look at what a likely to be the characteristics that make a good bow/arrow system for distance when accuracy is not an issue.
An example of a 'custom designed' flight bow used By Don Brown to set a world record of over 1336 yards in 1987. is given the at following link:
The approach to looking at flight shooting is to take a 'typical' target arrow and vary is properties one at a time to see how this affects how far the arrow can be shot.
The higher the speed at which the arrow leaves the bow then the
farther it goes. No surprises there. We need a bow with a high potential
energy storage in the limbs and an efficient use of this stored energy in
creating a high speed arrow.
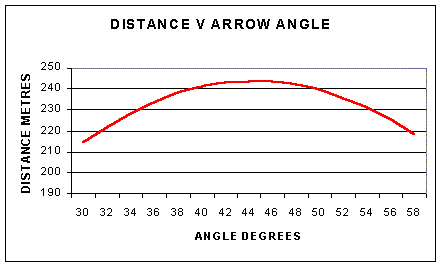If there were no aerodynamic forces then the angle for maximum distance
would be 45 degrees to the horizontal for any object. With aerodynamic
effects then the angle for maximum range becomes a function of the object
properties. For anything that could be called an arrow the angle for maximum
range is slightly under 45 degrees, between 44-45 degrees say. Shoot angles
for target archery in general only go up to around 10-15 degrees.
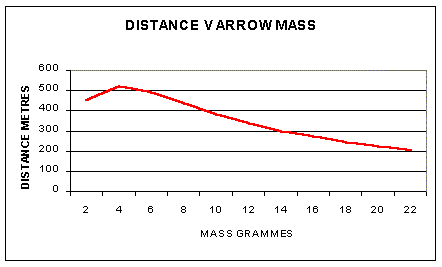Changing the arrow mass will change the speed of the arrow from
the bow. The approach in the above graph is to assume the kinetic energy
of the arrow leaving the bow is constant so changing the arrow mass also
changes its speed. (No allowance for changes in bow efficiency). As the
arrow decreases in mass and the bow exit speed increases then the arrow
up to a point goes farther. At some point the effect of drag deceleration
of the arrow will outweigh the increased initial speed so there is an 'optimum'
arrow mass for maximum range. This optimum mass will be much lighter than
any feasible arrow that can be made with current materials so in effect
the lighter the arrow the further it goes.
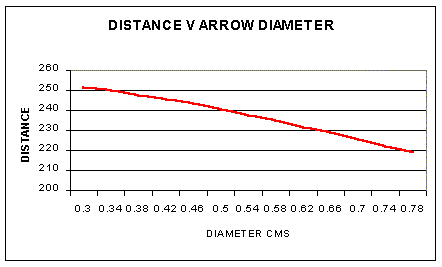Increasing the arrow diameter will increase the drag on the pile of the arrow and on the shaft. (the arrow mass is assumed independent of the diameter). Drag on the pile is all bad news as it slows the arrow and reduces the distance. Drag on the shaft is overall a benefit as it increases the vertical component of the total drag on the arrow (which a flight arrow is designed to maximize). The net effect is detrimental to range. To maximize range we want a thin an arrow as possible. A way to have a thin arrow with the high arrow acceleration we need for that high speed is to reduce the distance from the nock at full draw to where the arrow contacts the bow. This effectively 'stiffens' the arrow. In the Don Brown bow the grip is in front of the riser reducing the nock-bow distance while allowing for efficient use
of the muscles in the draw. A consequence of this approach is that the draw length is reduced. In order to get a high arrow speed with a smaller draw length you need a high draw weight and a bow design which stores a lot of energy at the start of the draw. The highly recurved limbs provide the latter bow characteristic.
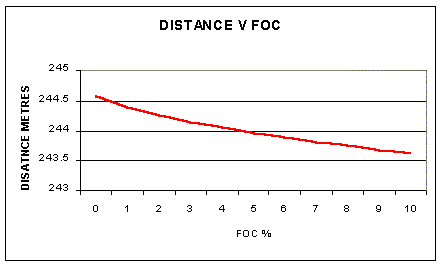The graph indicates that the lower the arrow FOC than the
the further it goes. This relates to two aspects of arrow flight, shaft
drag and arrow rotation rate. Flight arrows use the drag on the shaft to
maximise the vertical component of the total arrow drag (net upwards) and so they go further.The nearer the FOC is to zero the higher the shaft drag area and so the further the arrow flies. A lower FOC also reduces the rate at which the drag on the shaft and fletchings rotate the arrow again overall increasing the vertical component of the total arrow drag.
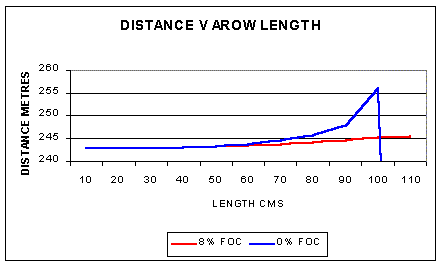For the target arrow (assumed 8% FOC) as the arrow gets longer there
is a marginal increase in arrow range. This results from the increasing
shaft area and the larger arrow moment of inertia increasing the drag on
the shaft. This shaft drag acts to slow the arrow down in the horizontal direction but also generates an upward force and net there is a benefit in increased distance. With the zero
FOC arrow you get the same effect but because there is no fletching action
from the shaft eventually the increased shaft drag results in the arrow loosing
all horizontal speed and parachuting down. As the arrow length increases
so does its mass which means a lower initial speed so there is a balance
to be struck on arrow length and mass. The mass effect on length will predominate
so a short arrow with overdraw is likely to be the preferred approach.
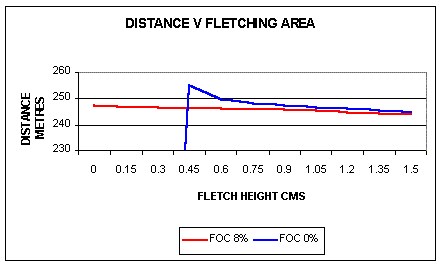The length of the fletching is assumed constant and the fletching
shape is taken to be a right angled triangle. The height of the rear
end of the fletching is therefore directly proportional to its area.
For the target (8% FOC) arrow increasing the fletching area has a small
effect, decreasing the maximum range. A bigger fletching area increases
the arrow rotation rate and therefore reduces the vertical component of the total drag as mentioned re FOC above. Target arrows have a lot of fletching action much of it coming from drag on the shaft. A flight arrow as mentioned above will have a low FOC and therefore small or zero shaft fletching action.
The blue curve in the graph represents how the fletching area affects
the range of a zero FOC arrow. Because of the Munk moment to get any distance
requires having enough fletching area to obtain 'stable' arrow flight, otherwise
the arrow just bombs. In theory the closer the fletching area lies to the minimum
the higher the arrow range. In practice you have to allow for the effect of any rotation the arrow has leaving the bow.
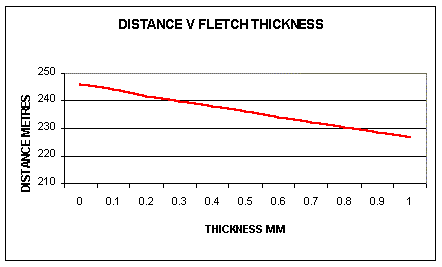The thicker the thickness of the fletching the more drag there is
slowing the arrow down. What is required is a very thin, rigid and straight fletching.
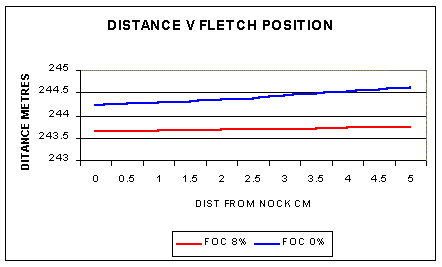The graph illustrates how the arrow range is effected by how
far the back of the (3.5 cm long by 1.5cm tall) fletching is from the
rear of the arrow. The fletching position affects the rate of rotation of
the arrow. For the both the target arrow and the 'flight' zero FOC arrow
the fletching position has only a marginal effect on arrow range. As the fletching
position moves forward the range marginally increases. For flight shooting
the standard arrow (fletching + shaft) has way too much fletching action
and even with the flight arrow (fletching area only) the standard arrow fletching
is too large. The following graph illustrates the effect of fletching position
with a smaller more sensibly sized fletching.
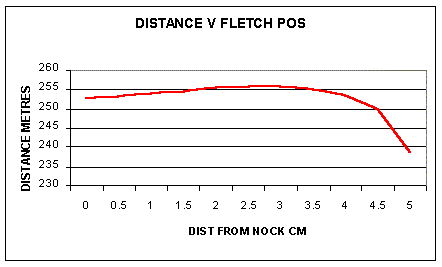With a correctly sized fletching the fletching position becomes
a 'tuneable' parameter with the maximum range obtained, in the example
above, with the rear of the fletching around 3 cms from the end of the
arrow.
The weight of the nock can have a number of influences on the performance of a flight arrow. Increasing the nock weight will make the arrow act stiffer possibly allowing for a lower spined (less diameter and less mass) arrow to be used. The nock weight can be used as an alternative way of varying the arrow FOC. Having weights on both ends of the arrow will affect the arrow moment of inertia and consequently the rotation rate of the arrow affecting its drag characteristics.
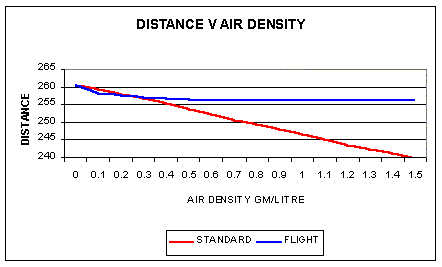The aerodynamic forces on an arrow are directly proportional to
the air density. With zero density, a vacuum, there are no aerodynamic
forces. For the standard target arrow which is shot with generally flat
trajectories drag, as far as distance is concerned, is not an issue. The
arrow is not designed to use drag efficiently as far as distance goes.
The above graph illustrates this, the higher the air density the lower
the range of the target arrow. The flight arrow, in contrast, is designed
to use drag on the arrow to increase it's range, so the effect of increasing air density
has only a marginal effect. In fact around the normal air density of 1.2 gms/litre the arrow range increases as the air density increases, so a drop in air density, e.g. high humidity, can reduce the distances being shot.
Last Revision 1 July 2009