Throw something up in the air and it goes up , stops and falls down again. Throw it up harder and it goes higher up and also takes longer to come down again. When you shoot an arrow at an angle you give the arrow some velocity in the (up) vertical direction and some velocity in the horizontal direction towards the target. The higher you raise the bow the higher the vertical velocity and the lower the horizontal velocity. The vertical velocity determines how long the arrow stays in the air, the horizontal velocity determines how far the arrow travels towards the target while it is in the air. To hit a specific vertical point you need the right combination of vertical and horizontal velocities i.e. the correct bow angle. You can hit any specific vertical point in two ways, you can have a high horizontal speed and short time in the air or a low horizontal speed with a long time in the air, i. e. you can hit a specific vertical point with two bow angles, usually called the "low" and "high" positions.
Gravity acts on the arrow as a whole always accelerating it downwards. What gravity does in the vertical plane is vary the direction in which the arrow is travelling overall. (ref) The total arrow velocity is the sum of the vertical and horizontal velocities. The arrow's speed in the horizontal plane continuously drops as it loses energy to the horizontal drag. The arrows vertical speed starts high, drops to zero and then increases as the arrow falls back to the ground. The overall arrow speed can therefore either be increasing or decreasing as the arrow approaches the target. Basically the higher the arrow trajectory the more likely it is the arrow will be speeding up as it nears the target.
As will be discussed later a fletched arrow is always trying to point into the net direction of the air flow over it. In the vertical plane the direction the arrow points is essentially defined by its "gravitational" trajectory. The arrow starts off pile upwards at some angle, rolls over to the horizontal and then ends up pile downwards at some angle. Because of this any initial arrow offset to the direction it is travelling or rotation in the vertical plane has a relatively minor effect on where the arrow ultimately hits the target. This is why "nocking point" tuning principally concerns itself with the arrow coming of the rest cleanly. The vertical arrow offset angle is only a secondary consideration.
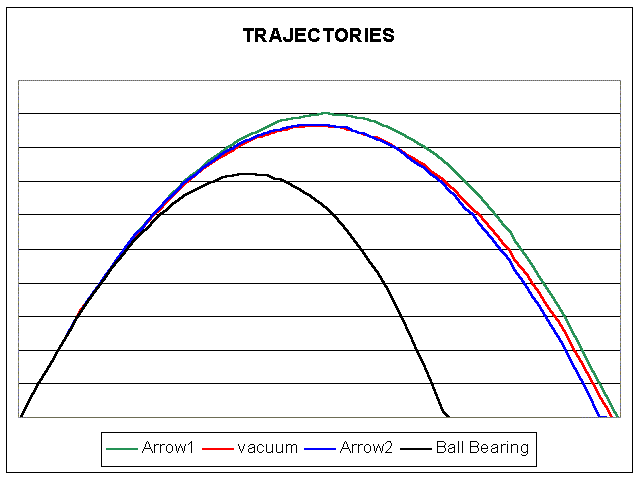
The following graph illustrates some trajectories.

Illustrated are trajectories of two different arrows and ball bearing all
shot at the same angle and the same initial speed. In a vacuum both arrows
and the ball bearing have the same trajectory (a parabola) and hit the ground
at the same spot. With air you have aerodynamic effects (drag and the Munk
effect) which affect the flight. All objects start off with the parabolic
flight path but increasingly deviate from it. The ball bearing 'falls short'
of the vacuum distance. With a typical target arrow the aerodynamic effects
'cancel out' to a large extent (both 'lift' and 'drag' forces are generated on the arrow) and the arrow hits at a much greater distance then the ball bearing. At short distances the trajectory is very close to the parabolic (vacuum) case. It's feasible to design an arrow which has a greatly reduced range with respect to a target arrow (e.g. flu-flu arrows) and equally possible to design an arrow which goes farther than the target arrow case (e.g. flight shooting arrows). Its possible to design an arrow where the effect of 'lift' outweighs the effect of 'drag' so the arrow range is actually greater than the vacuum case. Flight shooting arrows can be designed to 'use drag' so they can fly further if the air is denser and so the drag forces on the arrow are higher.
The arrow design requirements for long range conflict with the design requirements for accuracy.e.g. for arrow accuracy you want a high arrow FOC, for distance you want a low arrow FOC.
Last Revision 1 July 2009