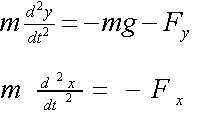 The figure gives the basic equations that describe the flight of a projectile in the
vertical plane.
The figure gives the basic equations that describe the flight of a projectile in the
vertical plane.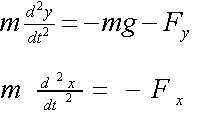 The figure gives the basic equations that describe the flight of a projectile in the
vertical plane.
The figure gives the basic equations that describe the flight of a projectile in the
vertical plane.
where 'm' is the mass, 'x' and 'y' are the horizontal and vertical distances, 'g' is the gravitational acceleration and 't' is time. 'F' is the drag force in the 'x' and 'y' directions.
The problem with calculating the trajectory of an arrow is 'F'. The drag force depends on velocity, orientation and rotation of the arrow and varies over the surface of the arrow. You cannot really ignore the motion and drag in the third 'z' direction either (though I am going to here). For an arrow these equations are not directly solvable. In other words you cannot write down an equation which gives you the height (Y) of the arrow at any distance (X). The only viable approach is to estimate 'what happens next' to the arrow over a short time interval and keep going around round the loop until you hit the target.
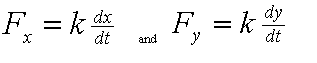 In order to get some idea of how a projectile flies with drag the assumptions
that the drag force is proportional to to the velocity and that the drag
properties of the flying object are very simple are often used because
although seriously wrong it does give you some solvable equations.
In order to get some idea of how a projectile flies with drag the assumptions
that the drag force is proportional to to the velocity and that the drag
properties of the flying object are very simple are often used because
although seriously wrong it does give you some solvable equations.
'k' is some sort of imaginary drag factor.
The solution to the equation then becomes:-
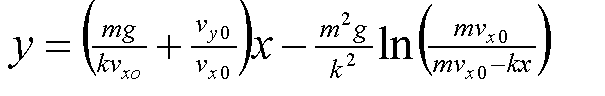
The projectile described by this equation has both 'x' and 'y' being zero when 't' is zero. Vxo and Vyo are the initial horizontal and vertical velocities. If 'V' is the total arrow speed out of the bow and 'A' is the bow angle to the horizontal then:
Vxo = VCos(A) and Vyo = VSin(A)
With respect to plotting an arrow flight trajectory, the above 'ballistic' approach has an number of incorrect assumptions (or simplifications if you like):-
1. The drag force is proportional to the arrow velocity.
2. Only gravity and drag forces affect the arrow trajectory
3. The drag properties of the arrow remain constant over the arrow flight.
4. The drag properties of the arrow are the same in all directions.
Re item 1. the drag force is actually proportional to the square of the arrow velocity. Unfortunately you cannot create the simple height - distance relationship above with drag proportional to the square of the velocity.
A ballistic model is based on the assumption that the flying object is a non rotating sphere of uniform density. This avoids the compications of 2,3 and 4 above. e.g. a ballistic model can't tell the difference between a golf ball, a glider and an arrow as far as flight trajectory is concerned. An arrow is anything but a sphere so any trajectories produced with a ballistic model will vary from approximate to illustrative. As its name implies BALListics relates to the flight of balls. You cannot sensibly apply a ballistic approach to the flight of an arrow.
Most, if not all 'Pin Tape' programs use a modified ballistic approach. In these the drag force is taken as proportional to the square of the velocity but the assumption that the arrow is spherical is retained.(Essentially the drag properties of the arrow are based on the arrow being rigidly mounted in a wind tunnel). You no longer have a single trajectory equation but have to use an iterative process over the time of arrow flight. This approach, from hearsay, seems to produce acceptably accurate 'sight marks' as long as the arrow trajectory is flat (high speed arrows over short distances). One factor that aids this is that as the distance increases then the required accuracy of the site mark goes down. e.g. if the pin tape line is 1 millimetre thick then this is equivalent to a 10 centimeter height variation at 90 metres. This approach cannot be used to sensibly estimate maximum arrow range or wind drift as in these areas the (ignored) arrow aerodynamic properties start to play a significant role. (e.g. maximum range is always underestimated and associated bow angle always too low).However with enough fiddling about with 'constants' it may be possible to get extend the distance over which acceptable sight marks are created - it depends on the ingenuity of the program author.
For a review of the ballistic approach see the following link (ballistics) (Bear in mind that although this approach can give acceptable values for pin tapes etc. it is only an empirical model and most of the 'theoretical content' is nonsense).
For general arrow flight trajectory calculatons see (ballistic calculator). It does try not to compensate for drag effects but is accurate enough for many practical considerations (like safe height for an archey hall)
See also arrow speed calculators for some arrow speed calculators.
Why does the ballistic approach work reasonably well with flat trajectories but go pear shaped with higher bow angles. The main reason relates to two assumptions made with the ballistic approach. The first assumption is that the total drag force on the arrow is equal to a constant multiplied by the square of the velocity. The second assumption is that the direction of the drag force is along the axis of the arrow (derived from the wind tunnel approach).
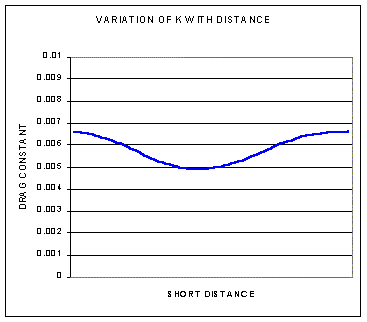 The ballistic assumed drag 'constant' isn't and varies from moment to moment through the flight of the arrow. The two graphs illustrate how the drag "constant"
typically varies. At short distances the constant is relatively constant so the ballistic assumption gives reasonable results,
The ballistic assumed drag 'constant' isn't and varies from moment to moment through the flight of the arrow. The two graphs illustrate how the drag "constant"
typically varies. At short distances the constant is relatively constant so the ballistic assumption gives reasonable results,
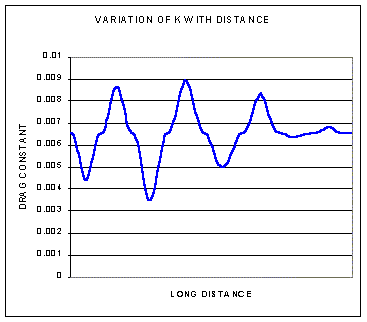 At longer distances you get much more variation in the value of the constant so the ballistic assumption doesn't work as well.
At longer distances you get much more variation in the value of the constant so the ballistic assumption doesn't work as well.
In practice for a free flying arrow the direction of the drag force is never along the axis of the arrow (the ballistic assumption) but varies over the flight through quite a large angle and at longer distances the drag direction acts on opposite sides of the arrow shaft. This topic is covered in the notes about drag. This creates a significant variation in the actual arrow flight trajectory to that predicted by the ballistic approach.
Last Revision 1 July 2009